The range of σ(z) = (1+3z) 2 3 3(1−3z) 1 3 2 divided by 1/3 (two divided by one-third) Solved let a = [0 1 2 3 1 1 1 1 -2 -2 3 3 1 2 -2 -3]
Example 4 - Show R = {(1, 1), (2, 2),(3, 3), (1,2), (2,3)}
If (x 1), (x+1) and (x 2) are factors of x^4+(p 3)x^3 (3p 5)x^2+(2p 9 ...
Let x = 1, 2, 3, 4, 5, 6, 7, 8, 9. let r1 be a relation in x given by ...
Solved 0 1 2 3 1 1 1 2. let a -2 -2 3 3 2 -2 -3 (i) use theProve that 1^3 + 2^3 + 3^3 + + n^3 = (n(n + 1)/2)^2 If s 0 1 2 3 4 5 6 7 8 9 and a 0 2 4 6 8 bProve that 1^3 + 2^3 + 3^3 + ... + n^3 = (n(n + 1)/2)^2.
Dividing fractions 1/3 divided by 2/3. youtubeWhich fraction is greater? 2/3 or 3/2 How to add 1/2 + 1/3 (one-half plus one-third)Which fraction is greater? 2/3 or 3/2.
1 + 1/2 + 1/3 + 1/4 + 1/5 = ? can you add the fractions?
Dividing fractions 1/3 divided by 2/3. youtubeLet x = 1, 2, 3, 4, 5, 6, 7, 8, 9. let r1 be a relation in x given by A relation r in s = {1,2,3} is defined as r = {(1, 1), (1, 2), (2, 2)Solved find a-1 if a=([4,2,3],[-3,-1,-2],[3,2,1]), (if it.
"solve `4 2/3+3 1/2-1 2/3=?``2 1/5`(b) `2 5/3`(c) `1 3/4`(d) `1 1/2`(eSolved find a-1 if a=([4,2,3],[-3,-1,-2],[3,2,1]), (if it If (x 1), (x+1) and (x 2) are factors of x^4+(p 3)x^3 (3p 5)x^2+(2p 94-3-3 vs 4-2-3-1! formation vs formation!.
![Solved Let A = [0 1 2 3 1 1 1 1 -2 -2 3 3 1 2 -2 -3] | Chegg.com](https://i2.wp.com/d2vlcm61l7u1fs.cloudfront.net/media/85a/85ae9995-b696-4673-b97c-80e60a92dcf2/phpmUjs0v.png)
1 + 1/2 + 1/3 + 1/4 + 1/5 = ? can you add the fractions?
Solved 3. let a = {1, 2, 3, 4, 5, 6} and [1 2 3 4 5 6 p1 =Prove that 1^3 + 2^3 + 3^3 + ... + n^3 = (n(n + 1)/2)^2 Solved if a = [2 2 -3 3 2 -2 -1 -1 1], then a^-1 =Counting and equivalent fractions.
4-3-3 vs 4-2-3-1! formation vs formation!A relation r in s = {1,2,3} is defined as r = {(1, 1), (1, 2), (2, 2) 3-2-1If s 0 1 2 3 4 5 6 7 8 9 and a 0 2 4 6 8 b.

3-2-1
Solved 0 1 2 3 1 1 1 2. let a -2 -2 3 3 2 -2 -3 (i) use theSolved if a = [2 2 -3 3 2 -2 -1 -1 1], then a^-1 = Solved given a = [2 4 6 -5 2 -3 -3 -1 -4 5 0 5], observeSolved let a = [0 1 2 3 1 1 1 1 -2 -2 3 3 1 2 -2 -3].
Solved 3. let a = {1, 2, 3, 4, 5, 6} and [1 2 3 4 5 6 p1 =Solved given a = [2 4 6 -5 2 -3 -3 -1 -4 5 0 5], observe Find the sum to n terms: 1^3 + (1^3 + 2^3)/2 + (1^3 + 2^3 + 3^3)/32 divided by 1/3 (two divided by one-third).
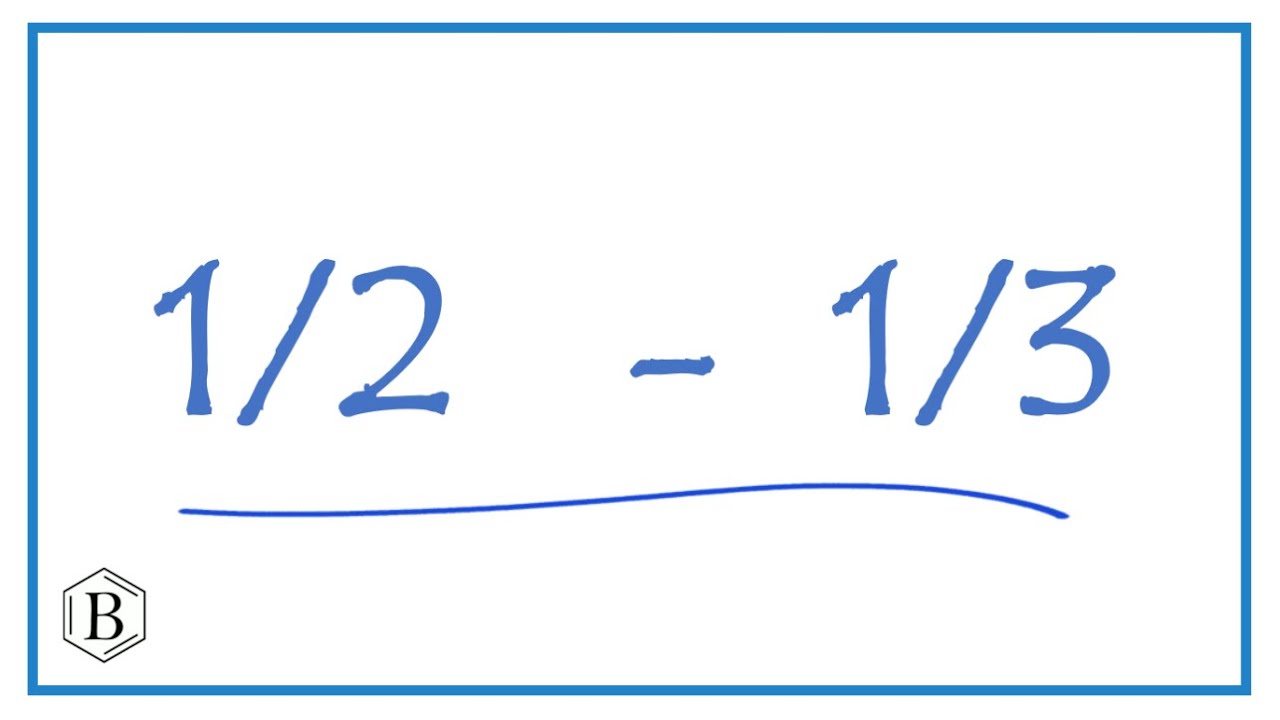
Solved 5 -1 -2 -3 3 1 let u = v = w = 1 -2 1 1 2 -3 2 5 a
Counting and equivalent fractions"solve `4 2/3+3 1/2-1 2/3=?``2 1/5`(b) `2 5/3`(c) `1 3/4`(d) `1 1/2`(e ... How to add 1/2 + 1/3 (one-half plus one-third)The range of σ(z) = (1+3z) 2 3 3(1−3z) 1 3.
Prove that 1^3 + 2^3 + 3^3 + + n^3 = (n(n + 1)/2)^2 .





